Estive relendo há pouco tempo o texto “DILEMMAS IN A GENERAL THEORY OF PLANNING”, de Rittel e Webber (1973), que é um texto muito interessante. Nele, os autores argumentam que os problemas sociais, tais como os enfrentados pelo planejamento, não são como os problemas relacionados à engenharia, matemática ou mesmo às ciências naturais e, portanto, não podem ser solucionados com os mesmos métodos. Segundo eles, os problemas enfrentados pelo planejamento podem ser considerados “capciosos” (wicked, no original).
Na solução de uma equação, ou numa partida de xadrez, sabe-se de antemão todas as condições do problema, as regras para sua resolução e os critérios necessários para saber se a solução foi correta, ou mesmo se pode ser ou não considerada uma solução. Nos problemas capciosos isso não se aplica.
Os autores listam as seguintes características para problemas desse tipo:
1. Não existe uma formulação definitiva para um problema capcioso
A informação necessária para entender o problema depende das hipóteses de solução desse problema. Por isso, “o entendimento do problema e sua resolução são concomitantes” (RITTEL; WEBBER, 2004, p. 56). O mesmo não acontece, por exemplo, nos problemas matemáticos, em que a formulação do problema pode ser feita sem que o mesmo comece a ser resolvido.
“A formulação de um problema capcioso é o problema” (RITTEL; WEBBER, 2004, p. 57)
2. Problemas capciosos não têm regra para definir quando parar
Como a formulação do problema acontece juntamente com sua solução, e como não há critérios que apontem quando um problema capcioso foi adequadamente descrito, o planejador sempre poderia “fazer melhor”, e prolongar a resolução do problema indefinidamente. As razões para não fazê-lo são externas à lógica própria do problema: falta de tempo, de recursos ou de paciência, por exemplo.
3. As soluções de problemas capciosos não são verdadeiras ou falsas, e sim boas ou más
Muitos atores têm interesses diferentes com relação às soluções dos problemas de planejamento, mas nenhum deles tem legitimidade para estabelecer critérios ou regras de decisão para definir quais decisões são corretas ou incorretas.
4. Não existe um teste completo para avaliar as conseqüências das soluções propostas
As soluções dos problemas capciosos, depois de implementadas, podem ter efeitos que se propagam através do tempo e do espaço de maneiras impossíveis de serem rastreadas. Esses efeitos não podem, portanto, ser avaliados com precisão, apesar de serem muitas vezes tão importantes quanto os efeitos imediatos.
5. Não é possível operar através de tentativa e erro para solucionar um problema capcioso
“Com os problemas capciosos, todas as soluções implementadas têm conseqüências. Elas deixas ‘rastros’ que não podem ser revertidos. Não se pode construir uma via expressa para ver como funciona, e depois corrigi-la facilmente se seu desempenho não for satisfatório” (RITTEL; WEBBER, 2004, p. 58)
6. Não existe um conjunto definido de alternativas possíveis
Quando se busca uma solução para um problema capcioso, um determinado número de alternativas é levantado, mas outra porção delas nem chega a ser cogitada. É uma questão de julgamento definir se o planejador deve continuar a tentar aumentar o leque de alternativas possíveis ou se deve dar-se por satisfeito com aquelas já levantadas.
7. Todo problema capcioso é único
Por mais que existam similaridades entre um problema e outro, sempre existe pelo menos uma característica importante e única em cada um deles. Cada problema tem sua peculiaridade, um aspecto próprio ou uma combinação de aspectos que não existia nos outros problemas enfrentados no passado. Isso dificulta a replicação de soluções, uma vez que estas podem não funcionar dentro de um contexto diferente daqueles em que foram originalmente aplicadas.
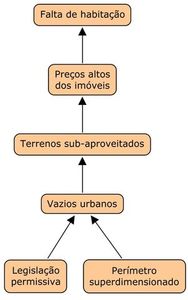8. Todo problema capcioso pode ser considerado um sintoma de outro problema
Na busca por definir com precisão o problema, deve-se analisar as relações causais existentes entre eles. Sendo assim, é possível definir o problema em muitos níveis de resolução, desde mais gerais até níveis mais específicos. Essa definição não pode ser feita em bases puramente lógicas.
9. A natureza de um problema pode ser explicada de muitas formas
Essa é especialmente importante: os autores argumentam que não é possível determinar com rigor científico as causas dos problemas capciosos, pelo fato de estes serem únicos (proposição 7) e pelo fato de ser difícil realizar experimentos rigorosos (proposição 5). Sendo assim, as explicações para os problemas acabam sendo definidas de forma um tanto arbitrária, ou seja, as pessoas acabam escolhendo as explicações que fazem mais sentido para elas (em oposição a explicações embasadas em pesquisas e critérios científicos). A visão de mundo do planejador acaba sendo o fator determinante para definir a explicação das causas dos problemas e, portanto, das soluções a serem recomendadas.
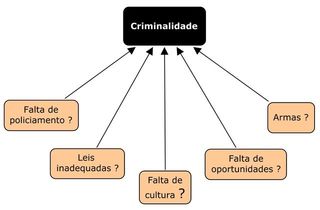Como exemplo, o autor cita o problema da criminalidade, que pode ser causado por falta de policiamento, alto número de criminosos, leis inadequadas, número excessivo de policiais, falta de cultura, deficiência de oportunidades, existência de armas, e por aí afora. Não há maneira científica de afirmar com segurança qual ou quais desses fatores causam a criminalidade porque (1) cada caso é um caso, ou seja, é único em relação aos demais (proposição 7); e (2) não é possível fazer experimentações rigorosas para cada caso que se deseja resolver (proposição 5), visto que uma tentativa de solução traz inevitavelmente conseqüências que podem ser desastrosas; em outras palavras, neste caso a refutação de uma hipótese não têm o mesmo valor que no método científico.
10. O planejador não tem o direito de estar errado
Decorrendo deste último pensamento, os autores concluem que o planejador não pode se dar ao luxo de errar, já que seu objetivo não é encontrar a verdade (como na ciência), mas sim melhorar o mundo em que as pessoas vivem.
Na mosca !!!!!!!!