Spacemate, Spacematrix e o estudo das densidade urbanas

Densidade Urbana é um dos assuntos mais caros aos urbanistas e planejadores urbanos, tendo (teoricamente) influência sobre a vitalidade dos espaços urbanos, movimento de pedestres e veículos, redes de abstecimento de água, esgoto e energia elétrica, etc. Alguns, como Acioly e Davidson (1998), atribuem até mesm maiores índices de criminalidade a densidades altas.

Entretanto, o assunto não é nada fácil de ser trabalhado teoricamente e incorporado à nossa prática, tendo em vista a enorme quantidade de aspectos envolvidos na questão. Mesmo a definição de densidade está sujeita a polêmicas e ambiguidades, com vários trabalhos dedicados a estudá-lo (veja, por exemplo, Churchman, 1999).

“Space, Density and Urban Form” (BERGHAUSER PONT; HAUPT, 2009) é um trabalho recente sobre o tema que, a meu ver, traz uma abordagem realmente inovadora e com um nível de rigor no tratamento da questão que raramento se vê por aí. Acredito que, em um futuro próximo, será considerado a principal referência quando se falar em densidades urbanas.

Os problemas dos indicadores tradicionais de densidade

Berghauser pont e Haut (2009) fazem uma revisão das medidas de densidade tradicionalmente usadas e mostram que nenhuma delas, por si só, é capaz de representá-la adequadamente. Um dos principais problemas na medição da densidade é a área utilizada como base para o cálculo. Diferentes critérios de demarcação podem introduzir distorções significativas nos resultados, uma vez que, quanto maior a área, maior é a sua heterogeneidade e maior é a quantidade de áreas não construídas (ruas, estradas, parques, corpos d’água, etc.), o que acabada impossibilitando a comparação entre áreas de tamanhos diferentes. Nesse sentido, embora existam os conceitos  de densidade bruta e líquida, os autores afirmam que esses conceitos ainda assim são ambíguos, dependendo das definições específicas adotadas em cada situação. Por isso, estabelecem neste trabalho uma série de unidades espaciais rigorosas sobre as quais construir os índices de densidade, e dentro das quais as comparações entre lugares diferentes seriam feitas adequadamente.

“Nós observamos que a intensidade da ocupação do solo (Índice de Aproveitamento) é mais eficaz mas ainda não nos permite diferenciar padrões diferentes de layouts. O mesmo pode ser dito sobre os outros índices de densidade discutidos aqui. Todos são, em certa medida, informativos, mas nenhum deles pode ser usado sozinho para descrever adequadamente propriedades espaciais na direção da definição de tipos urbanos através do uso de densidades” (BERGHAUSER PONT; HAUPT, 2009, p. 84)

Para uma explicação das medidas mais tradicionais de densidade, consulte o trabalho original de Berghauser pont e Haut (2009) e o post Taxa de Ocupação e Coeficiente de Aproveitamento, aqui no Urbanidades.

Outras medidas de densidade

Além das medidas mais tradicionais (Índice de Aproveitamento, Taxa de Ocupação e Número de Pavimentos), Berghauser pont e Haut (2009) utilizam outras medidas, algumas delas não muito conhecidas no contexto brasileiro. São elas:

Índice de Espaços Abertos (Open Space Ratio – OSR) – mede a proporção entre as áreas não construídas e a área total construída em um recorte, e busca dar uma indicação da pressão das áreas construídas sobre as áreas abertas. A figura abaixo ilustra o cálculo dessa medida: à esquerda estão as áreas abertas; à direita as áreas construídas. O OSR é calculado dividindo a primeira pela segunda.

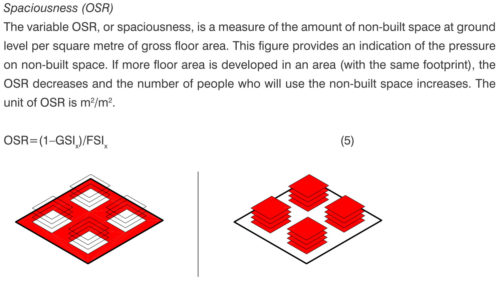
(Fonte: BERGHAUSER PONT; HAUPT, 2009, p. 96)

Densidade da Rede (Network Density) – definida como a quantidade de ruas dividida pela área, é expressa em metros (lineares) / metro quadrado. A Figura abaixo ilustra esse cálculo: a medida é resultante do comprimento total das vias (imagem da esquerda) dividida pela área total da unidade espacial (à direita).

(Fonte: BERGHAUSER PONT; HAUPT, 2009, p. 94)

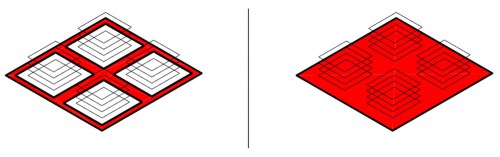
Largura (média) das ruas (b) e das quadras (w) (Mesh and profile width) – a largura média das quadras mede a distância média entre as vias em um tecido, e a largura média das ruas mede, como não poderia deixar de ser, a larguma média das ruas contidas no recorte de interesse, como pode ser visto na figura abaixo.

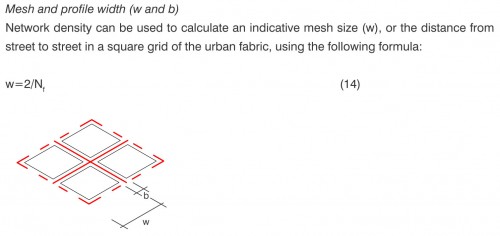
(Fonte: BERGHAUSER PONT; HAUPT, 2009, p. 97)

Uma definição multivariada da densidade

Uma definição precisa das unidades espaciais

Conforme comentado anteriormente, Berghauser pont e Haut (2009) introduzem definições bem precisas das unidades espaciais utilizadas para calcular densidades, o que permite que, quando comparações forem feitas, elas mantenham um mínimo de coerência no que está sendo medido.

Antes de descrever as unidades, entretanto, é importante explicar um conceito muito interessante que os autores introduzem e que perpassa todas as definições, sendo crucial para entendê-las e para compreender o porquê da necessidade de manter a coerência na definição das áreas-base: a Tara.

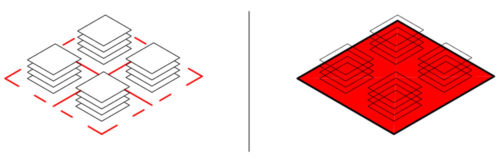
Tara – Apesar do nome soar estranho em português, nós usamos essa palavra num sentido muito parecido com o que eles estão utilizando. Segundo o Houaiss, “tara” significa, entre outras coisas, “desconto oferecido a cada mercadoria em função do peso de sua embalagem; o peso dessa embalagem; peso da carroceria de caminhão ou vagão de trem, quando vazios“. Tara, em restaurantes por quilo, é o peso do prato, descontado quando pesamos o prato juntamente com a comida e precisamos saber apenas o peso desta última. Dentro do SpaceMatrix, a Tara é usada para denotar os espaços que são acrescentados a uma unidade espacial quando considerada a unidade espacial mais ampla da qual a primeira faz parte. Por exemplo, quando passamos da unidade espacial “ilha” (quarteirão) para a unidade espacial “tecido”, adicionamos à primeira os espaços destinados a ruas, calçadas, calçadões, etc., que são a tara. O mesmo vale quando passamos do tecido para o bairro, quando passam a ser incorporados espaços como parques, praças, áreas de preservação, corpos d’água, etc.

Em termos mais específicos, a Tara é a relação entre a área que “sobra” e a área total (área da esquerda dividida pela área da direita, na imagem abaixo).

(Fonte: BERGHAUSER PONT; HAUPT, 2009, p. 96)

A partir disso, fica claro o porquê de não podermos (ou não devermos) comparar densidades calculadas, por exemplo, em cima de uma medida de tecido e uma medida de bairro. Esta última terá uma tara muito maior que a primeira, e portanto a densidade estará mais “diluída” na comparação. Comparando medidas calculadas sobre a mesma base minimiza esse risco.

Vamos, então, à explicação das unidades espaciais:

Lote – a parcela de propriedade. Não há muito que explicar aqui – refere-se ao lote como conhecemos e estamos acostumados a trabalhar, isto é, uma parcela de terra entendida como uma unidade imobiliária.

Ilha – ou quarteirão, é definida por um conjunto de lotes circundados por vias. Às vezes a ilha possui tara, mas isso não é comum no Brasil (a não ser, talvez, nas superquadras de Brasília, onde há uma porção das quadras que não faz parte dos “lotes” dos edifícios).

Tecido – um conjunto mais ou menos homogêneo de ilhas, incluindo portanto a rede viária que as separa. Não inclui, entretanto, grandes avenidas exclusivamente de passagem, viadutos, parques, grandes corpos d’água, campos esportivos, etc. Esses elementos são considerados a tara da próxima unidade espacial em relação ao tecido.

Bairro – Composto por tecidos mais os elementos citados acima.

SpaceMatrix

O SpaceMatrix é uma maneira engenhosa criada pelos autores para representar, em um único gráfico, várias características da densidade das áreas analisadas.Pela imagem abaixo podemos ver que uma área qualquer pode ser representada pelas três principais dimensões (Índice de Aproveitamento, Taxa de Ocupação e Densidade da Rede) em um ponto no espaço tridimensional, como uma espécie de “impressão digital da densidade” que representa uma combinação única dessas três medidas.

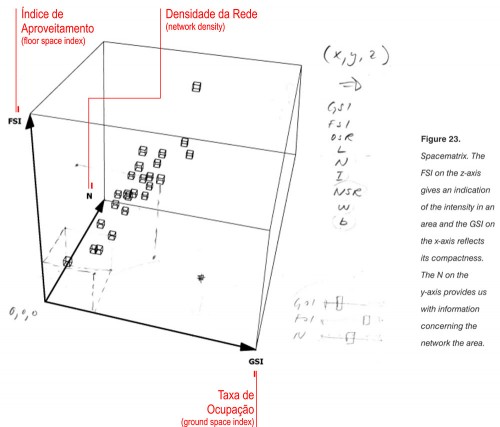
(Fonte: Adaptado de BERGHAUSER PONT; HAUPT, 2009, p. 98)

Entretanto, como o SpaceMatrix pode não ser facilmente entendido quando visualizado assim, os autores utilizam duas representações, equivalente a duas “faces” ou projeções do diagrama original, para comunicar melhor as relações entre as medidas.

O diagrama SpaceMate

O diagrama SpaceMate é uma das projeções do SpaceMatrix (e provavelmente a principal), correspondente à face FSI (ìndice de Aproveitamento) x GSI (Taxa de Ocupação). Conforme pode ser visto na figura abaixo, o eixo vertical apresenta o ìndice de Aproveitamento, enquanto que o eixo horizontal apresenta a Taxa de Ocupação. Um terceiro “eixo”, oblíquo, representa a quantidade média de pavimentos da área, obtida a partir da relação entre IA e TO. Pegue, por exemplo, a linha dos 5 pavimentos e percebemos que há infinitas combinações de IA e TO que poderiam ser feitas com 5 pavimentos, desde prédios mais “magrinhos” e com menor área construída (porção à esquerda e abaixo da linha) até prédios mais gordinhos e com maior IA (na porção à direita da linha). Inversamente, poderíamos ter lotes com um mesmo índice de aproveitamento e diferentes TOs. No caso, isso seria representado por uma linha horizontal que, à medida que fosse da esquerda (menor TO) para a direita (maior TO) cruzaria as linhas do número médio de pavimentos, sendo que estes últimos diminuiriam (resultando em edifícios mais “gordinhos e baixos ao invés de “magrinhos” e altos.

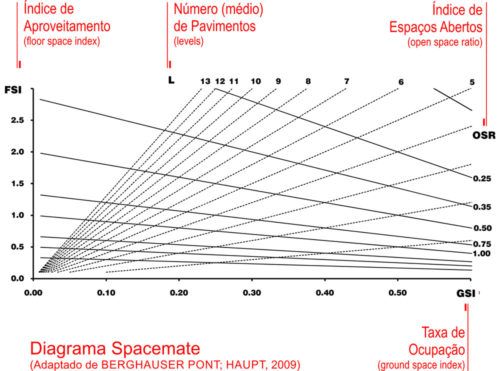
(Fonte: Adaptado de BERGHAUSER PONT; HAUPT, 2009, p. 99)

Outra visualização interessante permitida pelo SpaceMate é a da figura abaixo, que mostra as densidades de um mesmo tipo de ocupação calculadas com base em diferentes unidades espaciais. Note que nos pontos 1 e 2 a representação é a mesma, visto que não há tara quando se passa do lote à ilha. Entretanto, quando passamos para o tecido a área das vias é adicionada ao cálculo, o que acarreta uma diminuição da TO e do IA, sem entretanto diminuir o número médio de pavimentos. O mesmo acontece quando passamos para a representação 4, ao nível do bairro. Aqui fica ainda mais clara a importância, destacada anteriormente, de comparar lugares com base em unidades espaciais semelhantes para manter a consistência das medidas.

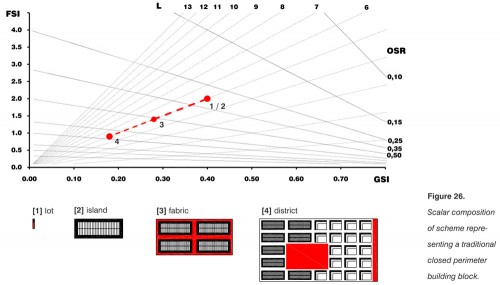
(Fonte: BERGHAUSER PONT; HAUPT, 2009, p. 100)

Muito interessante também são essas duas visualizações oferecida por van Nes et al (2012) (abaixo). Na primeira vemos três tipos de ocupação bastante distintos mas com mesmo IA e suas correspondentes localizações no SpaceMate. Os pontos mantêm-se em uma linha horizontal, por conta do IA constante, mas variam em TO e Número de Pavimentos.

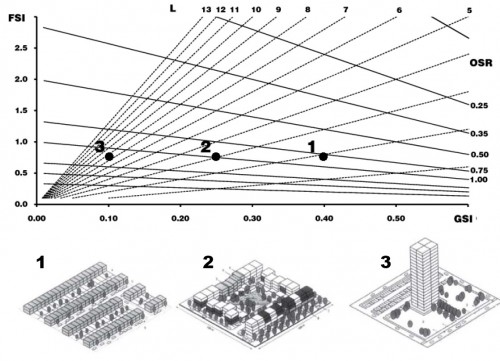
(Fonte: van NES; BERGHAUSER PONT; MASHHOODI, 2012, p. 4)

Através dela fica claro que o diagrama consegue captar características importante dos tipos edilícios e urbanos, de uma forma que nenhuma das medidas consegue fazer isoladamente.

Na segunda vemos uma tentativa de estabelecer uma classificação de tipos edilícios e de tecido. Cada área do diagrama representaria um dos tipos, indo desde aqueles mais baixos e com pouca área construída até os mais altos e muita área construída, passando por diversas situações intermediárias.

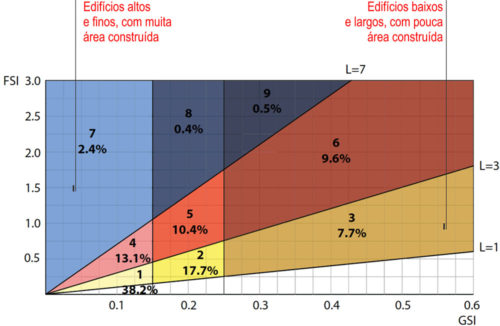
(Fonte: Adaptado de van NES; BERGHAUSER PONT; MASHHOODI, 2012, p. 14)

Através do SpaceMate, portanto, bem como das demais definições oferecidas por Berghauser e Haupt (2009), é possível analisar as densidades urbanas de forma muito mais precisa do que vem sendo feito usualmente.

Referências